Batch 3 - Class 141 - Induction
Preclass Exercise:
- Imagine an infinite chessboard that contains a positive integer in each square. If the value in each square is equal to the average of its for neighbors to the north, south, west and east, what should all the values look like?
- Answer: They are all equal. Proof by contradiction: assume that for any square, its value is different from one of its neighbors. Then there must exist a neighbor which has lower value. Now think about that neighbor - since the original square was larger, this neighbor must not have a neighbor which is even smaller. Thus, this chain must lead to a scenario where the numbers start to turn negative. Since this is not possible, all numbers must be equal.
- What would happen if we had 2000 points on a circle, and each number was average of its two nearest neighbors?Answer: Again the numbers would have to be all equal. Let kids work with smaller numbers to develop the intuition.
Attendance: Khushi, Arnav, Anishka, Damini, Anshi
Class Notes:
- (MC - 9 - 1) One square was cut from a 16x16 sqaure grid. Prove that the figure obtained can be dissected into trominos (3 squares in corner shape).
Instructor Notes: Let students think and about the problem, and come up with some answers. Note that simple divisibility by 3 doesn't suffice. After a bit, ask them to solve the problem for a 2x2 square. Once that is done, as them to do it for 4x4. They might do it by taking three possible cases. Guide them towards thinking about a 4x4 square as composition of 2x2 squares. Then 8x8 - by now the pattern must get intuitive.
- What can we say about any square?
- Careful: We have just said something about powers of 2, not an arbitrary square!
- Visualization
- How can we generalize the statement?
- Take the dominos analogy - to illustrate that the first domino requires a push (i.e. base case), and then every domino will fall if the previous one falls (i.e. induction step)
Introduce notion of variable. And then formalize the proof of this problem. (If 2^nx2^n square missing a square can be cut into trominos, then so can a 2^(n+1)x2^(n+1) square missing a square)
Introduce the terminology - Induction, Induction Hypothesis, Base, and Induction Step
- (Decade - 6 - 2.2) Another simple example: Upon being defeated and forced to abandon his castle forever, an evil magician casts a spell: if it rains one day over the castle, then it will rain the next day too. It happens to rain there today. What can we say about the future?
- Answer: It will rain forever. Get kids to identify the hypothesis, base and induction steps
- (Decade - 6 - 3.1) Prove that sum of first n odd natural numbers is n^2
- Instructor Notes: Clarify that the above statement is the induction hypothesis
- What should be the basis? Is that provable?
- What should be the induction step? Can you prove that step?
- (MC - 9 - 6) Into how many regions do n lines divide the plane, given that none of them are parallel, and not more than two intersect at a point.
- Kids will first have to form the hypothesis. Ask them to solve for a few cases to develop the hypothesis
- Now, ask them to prove the hypothesis using induction
Homework:
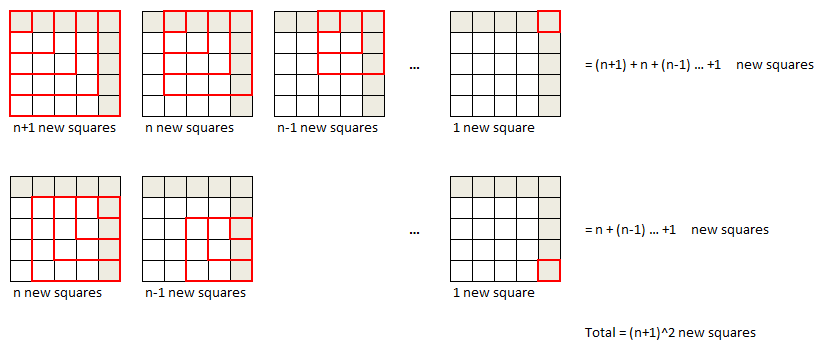
- How many squares does a 5x5 grid have? You have solved this problem before, but can you attempt it by induction? Can you generalize it for nxn square?
.png)
- Answer: 1^2+2^2+3^2+4^2+5^2
- Base case: 1x1 grid has only 1 square
- Induction Hypothesis: nxn grid has squares equal to sum of squares of first n natural numbers
- Induction Step: Assume nxn grid has the defined number of squares. Now lets add the (n+1)th row and column and try to count all the "new squares" this formed. It will incrementally be (sum of first n+1 natural numbers)+(sum of first n natural numbers) i.e. (n+1)^2.The easy way to look at the above sum (visually) is to see it as diagonals of a (n+1) x (n+1) square!
References:
Mathematical Circles (Russian Experience), by Dmitri Fomin, Sergey Genkin, Ilia Itenberg
A Decade of the Berkeley Math Circle. The American Experience, Volume 1. Zvezdelina Stankova, Tom Rike